Computational Complexity

What is?

Typically, computational complexity is the amount of time and memory needed to run algorithms. However, computational complexity theory is the study of the complexity of problems while algorithm analysis is the study of the complexity of algorithms.

Both these areas are highly related, since to design efficient algorithms it is essential to study their complexity. This is because, in most cases, we known that the complexity of a problem is less than the complexity of the algorithms.

Most common notations

Omega (Ω)

Represents the lower limit of complexity, that is, the best case. When we say that the complexity is Ω(f(n)), the algorithm cannot be more efficient than f(n) in terms of execution time.

Ω(g(n)) = { f(n) : ∃ c > 0, n0 > 0 | 0 ≤ cg(n) ≤ f(n), ∀ n ≥ n0}

O (O):

To express the idea of proportionality and worst cases in the execution time of the algorithm.

O(g(n)) = { f(n) : ∃ c > 0, n0 > 0 | 0 ≤ f(n) ≤ cg(n), ∀ n ≥ n0}

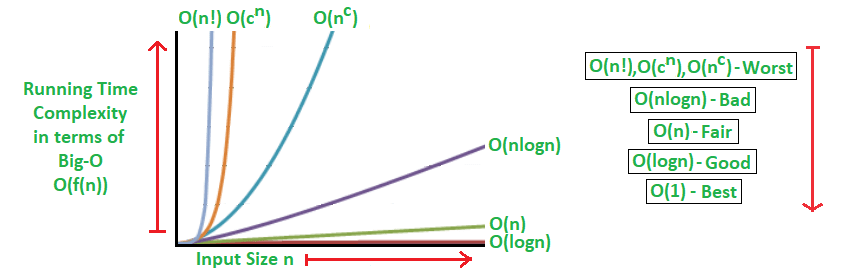
Basically, the idea is to use the letter O followed by a function over N that describes the growth of an algorithm. The faster the number of operations to process items grows, the worse the algorithm will perform [1]. See the chart below.

From FARIAS (2019)

Theta (Θ):

Represents a tight limit, that is, when the complexity in the best and worst cases is the same.

Θ(g(n)) = { f(n) : ∃ c1 > 0, c2 > 0, n0> 0 | 0 ≤ c1 g(n) ≤ f(n) ≤ c2 g(n) , ∀ n ≥ n0}

Big-O - Table

Notation	Complexity	Description	Example
O(1)	constant	There is no growth in the number of operations, as it does not depend on the volume of input data (n). Always execute the same instructions once.	direct access to an element of an array.
O(log n)	logarithmic	The growth of the number of operations is smaller than that of the number of items.	average case of the search algorithm in ordered binary trees
O(n)	linear	The growth in the number of operations is directly proportional to the growth in the number of items. Depend only on one parameter, which is the number of times a given loop (looping) is executed.	the search algorithm in a list/vector
O(n log n)	linearithmic or quasilinear	The result of operations (log n) executed n times.	the average case of the Quicksort sorting algorithm
O(n^2 )	quadratic	Occurs when data items are processed in pairs, often with repetitions within each other. With enough big data, it tends to get pretty bad. In general these algorithms have a for nested in another for.	processing items from a two-dimensional array
O(2^n )	exponential	In which as n increases, the analyzed factor (time or space) increases exponentially. It is not executable for very large values and is not useful from a practical standpoint.	search an unordered binary tree
O(n!)	factorial	The number of instructions executed grows very quickly for a small number of data.	an algorithm that generates all possible permutations of a list

From FARIAS (2019)

Here you can see a short summary: