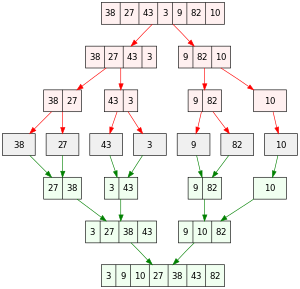
Merge Sort

Merge Sort is a sorting algorithm that follows the “divide and conquer” strategy to efficiently sort a list of elements. It works by recursively dividing the unsorted list into smaller sublists until each sublist contains only one element. Then, it repeatedly merges the sublists in a sorted order until the entire list is sorted.

How Merge Sort Works?

1. Divide: The unsorted list is divided into two halves recursively until each sublist contains only one element.
2. Conquer: Once the sublists are sufficiently small (containing only one element), they are merged back together in a sorted order.
3. Merge: During the merge phase, the sublists are merged pairwise, with elements being compared and rearranged to form larger sorted sublists. This process continues until the entire list is sorted.

From Wikipedia

Why Use Merge Sort

Merge Sort offers several advantages:

• It has a time complexity of O(n log n) in all cases, making it efficient even for large datasets.
• It guarantees stable sorting, meaning that elements with equal keys remain in their original order after sorting.
• Merge Sort is well-suited for sorting linked lists, as it does not require random access to elements.

Implement

First, we will need the lesseq macro. This macro is used for simplifying code and making it more readable.

• lesseq(A,B) compares if A is less than or equal to B.

#define lesseq(A,B) ((A) <= (B))

It will be used by the merge function. This function merges two sorted subarrays into one sorted array. It dynamically allocates memory for the temporary array R. It iterates through both subarrays, comparing elements and copying them to R in sorted order. It then copies the sorted elements from R back to the original array V, and deallocates memory for R.

void merge(int *V, int l, int m, int r){
  int *R=malloc(sizeof(int)*(r-l+1));
  int i=l,j=m+1,k=0;

  while(i<=m && j<=r)
  {
    if(lesseq(V[i],V[j]))
      R[k++]=V[i++];
    else
      R[k++]=V[j++];
  }

  while(i<=m)
      R[k++]=V[i++];
  while(j<=r)
      R[k++]=V[j++];


  k=0;
  for(i=l;i<=r;i++)
    V[i]=R[k++];
  free(R);
}

With that we can create the mergesort function, this function implements the merge sort algorithm recursively. It divides the array into two halves, sorts each half recursively using mergesort, and then merges the sorted halves using the merge function.

void mergesort(int *V,int l, int r){
  if (l>= r) return;
  int middle=(l+r)/2;
  mergesort(V,l,middle);
  mergesort(V,middle+1,r);
  merge(V,l,middle,r);
}

That’s it! You have your merge sort!

The Big-O notation

Merge Sort has a time complexity of O(n log n) for both the average and worst-case scenarios, making it highly efficient for sorting large datasets. It is particularly suitable for scenarios where stable sorting and consistent performance are required. Additionally, Merge Sort has a space complexity of O(n), as it requires additional space proportional to the size of the input list for temporary storage during the sorting process.

Data Structure	Time Complexity								Space Complexity
	Average				Worst				Worst
	Access	Search	Insertion	Deletion	Access	Search	Insertion	Deletion
Merge Sort	O(n log n)	O(n log n)	O(n log n)	O(n log n)	O(n log n)	O(n log n)	O(n log n)	O(n log n)	O(n)

Code

/*Giovanna Borges Bottino giovannabbottino@gmail.com*/

#include <stdio.h>
#include <stdlib.h>

#define less(A,B) ((A) < (B))
#define lesseq(A,B) ((A) <= (B))
#define exch(A,B) { int t; t=A;A=B;B=t; }
#define cmpexch(A,B) { if (less(B,A)) exch(A,B); }

void printList(int list[], int i);
void mergesort(int *V,int l, int r);
void merge(int *V, int l, int m, int r);

int main(){
    int n;
    while(1){
        scanf(" %d", &n);
        if (n == 0){
            break;
        }
        int *p=malloc(sizeof(int)*(n * 2));
        
        for (int i=0;i<n;i++){
            scanf(" %d", &p[i]);
        }
        
        mergesort(p,0, n-1);
        printList(p, n);
        
        free(p);
    }
    
    return 0;
}

void merge(int *V, int l, int m, int r){
  int *R=malloc(sizeof(int)*(r-l+1));
  int i=l,j=m+1,k=0;

  while(i<=m && j<=r)
  {
    if(lesseq(V[i],V[j]))
      R[k++]=V[i++];
    else
      R[k++]=V[j++];
  }

  while(i<=m)
      R[k++]=V[i++];
  while(j<=r)
      R[k++]=V[j++];


  k=0;
  for(i=l;i<=r;i++)
    V[i]=R[k++];
  free(R);
}

void mergesort(int *V,int l, int r){
  if (l>= r) return;
  int middle=(l+r)/2;
  mergesort(V,l,middle);
  mergesort(V,middle+1,r);
  merge(V,l,middle,r);
}

void printList(int list[], int i){
    int j;
    for (j=0;j<i; j++){
        printf("%d ", list[j]);
    }
    printf("\n");
}

References

[1] Wikipedia. Merge Sort. Available at: https://en.wikipedia.org/wiki/Merge_sort. Accessed: March 01, 2024.