Tree
What is a tree?
When you think of a tree, what do you expect? To me, it’s a plant, I can also define anything resembling a tree as something that has divisions and branches, root and leaf. We are going to follow that logic.
Now try connecting it to data structures. How could you implement this?
A tree is a nonlinear hierarchical data structure in which elements are not stored in contiguous memory locations. In a tree each elements are nodes connected by edges where no reference is duplicated and none points to the start [2].
From TUTORIALSPOINT
Why use a tree?
They are used for a faster response time during a search.
But first there are some important terms we need to know about trees.
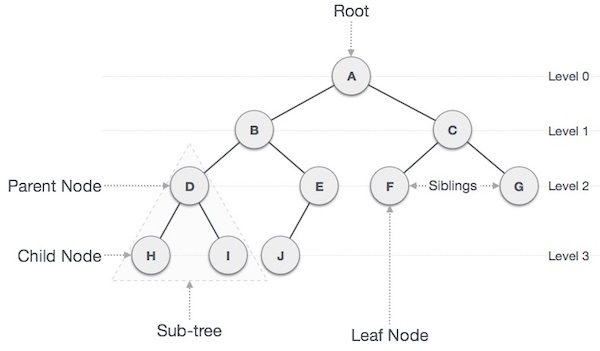
Tree Terminologies
-
Root − The node at the top of the tree is called root. There is only one root per tree and one path from the root node to any node.
-
Parent − Any node except the root node has one edge upward to a node called parent.
-
Leaf − The node which does not have any child node is called the leaf node.
-
Child − The node below a given node connected by its edge downward is called its child node.
-
Edge - It is the link between any two nodes.
-
Keys − Key represents a value of a node based on which a search operation is to be carried out for a node.
-
Height of a Tree - The height of a Tree is the height of the root node or the depth of the deepest node.
-
Levels − Level of a node represents the generation of a node. If the root node is at level 0, then its next child node is at level 1, its grandchild is at level 2, and so on.
-
Height of a Node - The height of a node is the number of edges from the node to the deepest leaf (ie. the longest path from the node to a leaf node).
-
Depth of a Node - The depth of a node is the number of edges from the root to the node.
-
Degree of a Node - The degree of a node is the total number of branches of that node.
-
Forest - A collection of disjoint trees is called a forest. You can create a forest by cutting the root of a tree.
-
Path − Path refers to the sequence of nodes along the edges of a tree.
-
Subtree − Subtree represents the descendants of a node.
-
Traversing − Traversing means passing through nodes in a specific order.
Tree Traversal
- Inorder: Visit all the nodes in the left, then the root node and finally all the nodes in the right.
- Preorder: Visit the root node, then all the nodes in the left and finally all the nodes in the right.
- Postorder: Visit all the nodes in the left, then all the nodes in the right and finally the root node.
Types of Tree
Binary Tree
In a binary tree, the nodes can have a maximum of two children.
Binary Search Tree (BST)
A binary tree subtype, arranged so that each node on the left side must have a value less than the value of its parent node. Inverse logic applies to the right side, which must have a higher value than its parent node. In this way, it allows faster search, query and addition / removal of data.
AVL Tree
The Adelson-Velsky-Landis (AVL) tree is a self-balancing binary search tree in which each node maintains extra information called a balance factor whose value is either -1, 0 or +1. The child nodes are rebalanced when the height difference exceeds one.
B-Tree
A generalized form of the binary search tree. Unlike a binary tree, allows its nodes to have more than two child and each node can contain more than one key. The B-Tree is a type of self-balancing tree that sorts data in logarithmic time.
Implement a Binary Search Tree
We’re going to implement a Binary Search Tree using node object and connecting them through references. First, we create a Node with two pointers, the left and the right.
typedef struct node{
int data;
struct Node *left;
struct Node *right;
} Node;
Implement the function to create a Node.
Node *createNode(int data){
Node* node = (Node *)malloc(sizeof(Node));
node->data = data;
node->left = NULL;
node->right = NULL;
return node;
}
Now we are ready to create the tree. It’s a Binary Search Tree, so to populate our tree we need to check the size of the data. For that we are going to make recursive calls. Is it bigger then the parent? So it is going to the right. Is it smaller then the parent? Left then. There is no parent? Create the node.
Node *createTree(Node *node, int data){
if (node == NULL)
return createNode(data);
if (data < node->data)
node->left = createTree(node->left, data);
else if (data > node->data)
node->right = createTree(node->right, data);
return node;
}
To remove it’s a litle more complicated. First, we need to make sure that there is a tree, is there a Node? After that we need to find the Node in the tree that contains that data. Is the data smaller then the data of Node? Go left. Is the data bigger then the data of the Node? Go right. Is it the data? Remove it.
Node *removeNode(Node *node, int data){
if (node==NULL){
return NULL;
}
if ( key < node->key){
node->left = removeNode(node->left, key);
} else if ( key > node->key){
node->right = removeNode(node->right, key);
} else {
// remove it
}
}
But how we remove it?
We need to know if this Node is a Leaf, it easier to just free a Leaf. When there is a child but only in one side, update the location of the child. He is going to be the new Node.
if(node->left == NULL){
Node *aux = node->right;
free(node);
return aux;
} else if(node->right == NULL){
Node *aux = node->left;
free(node);
return aux;
} else{
// child on both sides
}
return node;
The last case is when there is child on both sides. When this happens get the inorder successor. How? Lets make a recursive function to that.
Node *inorderSuccessor(Node *node) {
while (node && node->left != NULL)
node = node->left;
return node;
}
Now, replace the node key with the inorder successor key and remove the inorder from the original position.
Node *inorder = inorderSuccessor(node->right);
node->key = inorder->key;
node->right = removeNode(node->right , inorder->key);
The final function is similar to this.
Node *removeNode(Node * node, int key){
if (node==NULL){
return NULL;
}
if ( key < node->key){
node->left = removeNode(node->left, key);
} else if ( key > node->key){
node->right = removeNode(node->right, key);
} else {
if(node->left == NULL){
Node *aux = node->right;
free(node);
return aux;
} else if(node->right == NULL){
Node *aux = node->left;
free(node);
return aux;
} else{
Node *inorder = inorderSuccessor(node->right);
node->key = inorder->key;
node->right = removeNode(node->right , inorder->key);
}
return node;
}
}
You alredy know how to access, insert and delete a Node from the BST. Now let’s, understand the logic for Inorder, Preorder and Posorder. To achieve this, we will use some print.
Like we said before in tree traversal, each one follows a order. Inorder is left and then root, Preorder is root and then left and finally Postorder left and then right.
Using a recursive function and prints we can just make recursives calls to print first the left, then the root and finally the right.
void printTreeInorder(Node * node){
if (node){
printTreeInorder(node->left);
printf("%d ", node->key);
printTreeInorder(node->right);
}
}
And the same logic aplies to the Preorder and Postorder. Make recursives calls to print in the chosen order.
void printTreePreorder(Node * node){
if (node){
printf("%d ", node->key);
printTreePreorder(node->left);
printTreePreorder(node->right);
}
}
void printTreePostorder(Node * node){
if (node){
printTreePostorder(node->left);
printTreePostorder(node->right);
printf("%d ", node->key);
}
}
The Big-O notation
| Data Structure | Time Complexity | Space Complexity | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Average | Worst | Worst | |||||||
| Access | Search | Insertion | Deletion | Access | Search | Insertion | Deletion | ||
| Binary Search Tree | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(n) | O(n) | O(n) | O(n) | O(n) |
| B-Tree | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(n) |
| AVL Tree | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(n) |
Code
/*
* Giovanna Borges Bottino
* giovannabbottino@gmail.com
*/
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
typedef struct node{
int key;
struct node *left;
struct node *right;
} Node;
Node * createNode(int key);
Node * createTree(Node * tree, int key);
Node * removeNode(Node * tree, int key);
Node * inorderSuccessor(Node * node);
void printTreeInorder(Node * node);
void printTreePreorder(Node * node);
void printTreePostorder(Node * node);
int main(){
Node * tree = NULL;
int key = 10;
tree = createTree(tree, key);
printTreePreorder(tree);
printTreeInorder(tree);
printTreePostorder(tree);
removeNode(tree, key);
return 0;
}
Node *createNode(int key){
Node* node = (Node *)malloc(sizeof(Node));
node->key = key;
node->left = NULL;
node->right = NULL;
return node;
}
Node *createTree(Node * node, int key){
if (node == NULL)
return createNode(key);
if (key < node->key)
node->left = createTree(node->left, key);
else if (key > node->key)
node->right = createTree(node->right, key);
return node;
}
Node *removeNode(Node * node, int key){
if (node==NULL){
return NULL;
}
if ( key < node->key){
node->left = removeNode(node->left, key);
} else if ( key > node->key){
node->right = removeNode(node->right, key);
} else {
if(node->left == NULL){
Node *aux = node->right;
free(node);
return aux;
} else if(node->right == NULL){
Node *aux = node->left;
free(node);
return aux;
} else{
Node *inorder = inorderSuccessor(node->right);
node->key = inorder->key;
node->right = removeNode(node->right , inorder->key);
}
return node;
}
}
Node *inorderSuccessor(Node * node) {
while (node && node->left != NULL)
node = node->left;
return node;
}
void printTreeInorder(Node * node){
if (node){
printTreeInorder(node->left);
printf("%d ", node->key);
printTreeInorder(node->right);
}
}
void printTreePreorder(Node * node){
if (node){
printf("%d ", node->key);
printTreePreorder(node->left);
printTreePreorder(node->right);
}
}
void printTreePostorder(Node * node){
if (node){
printTreePostorder(node->left);
printTreePostorder(node->right);
printf("%d ", node->key);
}
}
References
[1] PROGRAMIZ. Tree Data Structure. Programiz. Available at: https://www.programiz.com/dsa/trees. Accessed: January 04, 2022.
[2] TUTORIALSPOINT. Data Structure and Algorithms - Tree. TutorialsPoint. Available at: https://www.tutorialspoint.com/data_structures_algorithms/tree_data_structure.htm. Accessed: January 04, 2022.