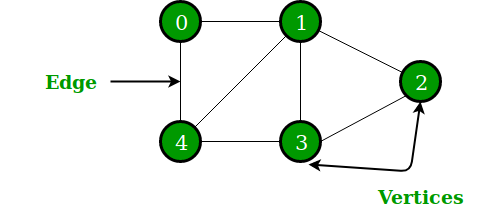
Graph

What is a Graph?

Consider a spider web—a network of dots and lines. Each dot is linked to another through a line, creating a complex and diverse set of connections that goes beyond the simplicity of lists or trees.

In the realm of computer science, graphs provide a visual representation of interconnected elements. The dots in this scenario are formally known as vertices (V), while the lines that connect them are referred to as edges (E).

When constructing a graph on a computer, it’s crucial to design a plan outlining how the dots and lines will be stored. This plan serves as a guide, helping the computer comprehend and remember the multitude of connections among the dots [1].

In essence, a graph simplifies the depiction of relationships by connecting dots with lines. This approach offers a captivating method for computers to understand the intricate web of connections between various entities, much like the intricate structure of a spider web.

From GEEKSFORGEEKS

Why use a Graph?

Graph theory is like a superpower that helps us understand and solve problems in different areas.

• Electrical Engineering:

Imagine you’re designing a circuit for gadgets. Graph theory helps in creating the perfect connections between the electronic parts. We call these connections “topologies,” and they have names like star, bridge, series, and parallel.

• Computer Science:

In the world of computers, graph theory is like a algorithm! Think of it as a set of instructions that help computers solve problems. Algorithms like Kruskal’s, Prim’s, and Dijkstra’s make sure things run smoothly.

• Computer Network:

Have you ever wondered how all the computers in your house or school are connected? Graph theory plays a big role! It helps us understand how these computers talk to each other in a network.

• Science:

Even in the tiniest things, like the structure of molecules or DNA, graph theory is there! It helps scientists draw pictures (graphs) to understand how these building blocks connect and work together.

Types of Graphs

Knowing that the number of vertices are V and number of edges are E here are the types of graphs.

• Undirected Graphs:

In an undirected graph with V vertices, the number of potential connections is determined by E. Each friend is a vertex, and the relationships between friends form edges. The undirected graph allows for bidirectional connections, illustrating a friendly network with a maximum of E = V * (V - 1) / 2 possible edges.

• Directed Graphs:

For a directed graph with V vertices and E edges, each edge represents a one-way connection between two vertices. The maximum number of directed edges is E = V * (V - 1), showcasing the unidirectional nature of the connections.

• Star Graphs:

In a star graph with a central point linked to other points, there are V - 1 edges radiating from the center to the outer points. Thus, the number of edges in a star graph is E = V - 1.

• Parallel Graphs:

For parallel graphs featuring two independent roads or paths, the number of edges is directly related to the number of vertices. The maximum number of edges in parallel graphs is E = V * (V - 1).

• Tree Graphs:

A tree graph with V vertices will have exactly V - 1 edges, creating a hierarchical structure resembling a family tree.

• Cyclic and Acyclic Graphs:

In cyclic graphs, the number of edges can vary but is limited by the number of vertices. The maximum number of edges in a simple cyclic graph is E = V * (V - 1). Acyclic graphs, being devoid of loops, have a maximum of E = V - 1 edges.

Understanding the relationship between the number of vertices and edges allows for a more precise characterization of these graph structures, providing insights into their connectivity and complexity.

Implement a Graph

The code starts by including a definition of a structure called Node. A Node represents a house, and it has a number (data) and a connection to the next house (next).

typedef struct Node {
    int data;
    struct Node* next;
} Node;

Another structure that need to be defined is the Graph. This represents the entire map of our city. It contains the number of houses (vertices) and a list (adjacency_list) that shows how the houses are connected.

typedef struct Graph {
    int vertices;
    Node** adjacency_list;
} Graph;

Here, a function called createNode is defined. It creates a new house (Node) with a specific number (data).

Node* createNode(int data) {
    Node* newNode = (Node*)malloc(sizeof(Node));
    newNode->data = data;
    newNode->next = NULL;
    return newNode;
}

The createGraph function is like creating a big map (Graph) with a certain number of houses (vertices). It also prepares space for the connections (adjacency_list) between the houses.

Graph* createGraph(int vertices) {
    Graph* graph = (Graph*)malloc(sizeof(Graph));
    graph->vertices = vertices;

    // Allocate memory for the adjacency list
    graph->adjacency_list = (Node**)malloc(vertices * sizeof(Node*));

    // Initialize the adjacency list
    for (int i = 0; i < vertices; ++i) {
        graph->adjacency_list[i] = NULL;
    }

    return graph;
}

The addEdge function is like drawing a passage between two houses on our city. It connects one house to another and also connects the other house back (assuming a two-way connection).

void addEdge(Graph* graph, int src, int dest) {
    // Add an edge from src to dest
    Node* newNode = createNode(dest);
    newNode->next = graph->adjacency_list[src];
    graph->adjacency_list[src] = newNode;

    // Add an edge from dest to src (assuming an undirected graph)
    newNode = createNode(src);
    newNode->next = graph->adjacency_list[dest];
    graph->adjacency_list[dest] = newNode;
}

The printGraph function is like reading the entire map and telling everyone how the houses are connected. It goes through each house and lists its connections.

void printGraph(Graph* graph) {
    for (int i = 0; i < graph->vertices; ++i) {
        printf("Vertex %d:", i);
        Node* current = graph->adjacency_list[i];
        while (current != NULL) {
            printf(" -> %d", current->data);
            current = current->next;
        }
        printf("\n");
    }
}

The Big-O notation

Data Structure	Time Complexity								Space Complexity
	Average				Worst				Worst
	Access	Search	Insertion	Deletion	Access	Search	Insertion	Deletion
Undirected Graph	O(V)	O(V + E)	O(1)	O(1)	O(V)	O(V + E)	O(1)	O(1)	O(V + E)
Directed Graph	O(V)	O(V + E)	O(1)	O(1)	O(V)	O(V + E)	O(1)	O(1)	O(V + E)
Star Graphs	O(V)	O(V)	O(1)	O(1)	O(V)	O(V)	O(1)	O(1)	O(V)
Parallel Graphs	O(V)	O(V)	O(1)	O(1)	O(V)	O(V)	O(1)	O(1)	O(V)
Tree Graphs	O(V)	O(V)	O(1)	O(1)	O(V)	O(V)	O(1)	O(1)	O(V)
Cyclic and Acyclic Graphs	O(V)	O(V + E)	O(1)	O(1)	O(V)	O(V + E)	O(1)	O(1)	O(V + E)

Code

/*
 * Giovanna Borges Bottino 
 * giovannabbottino@gmail.com
 */

#include <stdio.h>
#include <stdlib.h>

typedef struct Node {
    int data;
    struct Node* next;
} Node;

typedef struct Graph {
    int vertices;
    Node** adjacency_list;
} Graph;

Node* createNode(int data) {
    Node* newNode = (Node*)malloc(sizeof(Node));
    newNode->data = data;
    newNode->next = NULL;
    return newNode;
}

Graph* createGraph(int vertices) {
    Graph* graph = (Graph*)malloc(sizeof(Graph));
    graph->vertices = vertices;

    graph->adjacency_list = (Node**)malloc(vertices * sizeof(Node*));

    for (int i = 0; i < vertices; ++i) {
        graph->adjacency_list[i] = NULL;
    }

    return graph;
}

void addEdge(Graph* graph, int src, int dest) {
    Node* newNode = createNode(dest);
    newNode->next = graph->adjacency_list[src];
    graph->adjacency_list[src] = newNode;

    newNode = createNode(src);
    newNode->next = graph->adjacency_list[dest];
    graph->adjacency_list[dest] = newNode;
}

void printGraph(Graph* graph) {
    for (int i = 0; i < graph->vertices; ++i) {
        printf("Vertex %d:", i);
        Node* current = graph->adjacency_list[i];
        while (current != NULL) {
            printf(" -> %d", current->data);
            current = current->next;
        }
        printf("\n");
    }
}

int main() {
    Graph* graph = createGraph(5);

    addEdge(graph, 0, 1);
    addEdge(graph, 0, 4);
    addEdge(graph, 1, 2);
    addEdge(graph, 1, 3);
    addEdge(graph, 1, 4);
    addEdge(graph, 2, 3);
    addEdge(graph, 3, 4);

    printGraph(graph);

    return 0;
}

References

[1] GEEKSFORGEEKS. Applications of Graph Data Structure. Available at: https://www.geeksforgeeks.org/applications-of-graph-data-structure/. Accessed: January 28, 2024.